The Forty-Seventh Proposition of Euclid
(A.K.A. The Pythagorean Theorem)
Every man who passes through the portals of a Masonic lodge to become a brother of the Craft hears that
the 47th proposition of Euclid is one of the important symbols of Masonry.
That proposition is the one most people these days call the Pythagorean Theorem, the rule that in every
right triangle, the square of the longest side is equal to the squares of the other two sides. There are
plenty of propositions in Euclid, and no doubt any one of them could have been picked out of the Elements
of Geometry and turned into a Masonic symbol. For that matter, since geometry as a lump is already part
of our symbolism, why pick on this one proposition? The reason is that it used to be one of the basic
tools of the operative craft back in the Middle Ages.
It's easy to forget that designing and constructing a building of any size in those days involved
complexities that architects and contractors today don't have to deal with. Nowadays the architect
draws up blueprints, and then the builders follow those. In the Middle Ages, though, blueprints didn't
exist yet ‐ in fact, for many centuries you couldn't even get paper in Europe. People had to
make do with parchment, which is made from sheepskin and costs too much to use for anything as temporary
as building plans. That's why we have tracing boards in the Craft today.
In the old days the master mason in charge of a building project would have a big wooden board on site
and trace out designs on it for the workmen to follow. That's what a tracing board originally
The Forty-Seventh Proposition of Euclid
(A.K.A. The Pythagorean Theorem)
was.
The diagrams were drawn in three colors; chalk for white lines, charcoal for black lines, and clay for
red lines. Those brothers who know their ritual will remember that these have been given other meanings
in our modern speculative Craft, but they started out as drawing materials on medieval worksites.
It's one thing to lay out a drawing on a wooden board, though, and quite another to turn it into a
ground plan on the building site. Today's contractors do that with surveying tools, but our
operative brethren in the Middle Ages didn't have those. The efficient surveying tools the Romans
used in their day had been forgotten during the barbarian invasions and working builders in medieval
England didn't even know they had existed. Instead, they used geometry.
We happen to know a lot about the geometry they used because of a bit of luck back in the 1970s. A British
real estate company bought some property for a housing development at Norton Priory in England, not far
from Liverpool. English law requires you to have an archeologist and see if there's anything that
needs digging up before the bulldozers arrive. The archeologist found the ruins of a twelfth century
church, and the developers decided it would make a great sales gimmick. They turned the site into a park
in the middle of the development, and all the sales literature talked about the romantic medieval ruin.
It was a big success for the developers, but the archeologists also hit pay dirt; between the ruins and
old records they found in local archives and they were able to figure out how the master mason who built
the church laid it out.
His name was Hugh de Cathewik, and in the spring of 1134, he was hired by the monks of the Priory of St.
Bertelin to build a stone church. The contract still exists! He and his two deacons went to work before
dawn on the morning of the feast day of St. Bertelin using two staffs and the light of the rising sun
(as explained in the previous installment of this series) to lay out an east‐west line on the ground
where the church would be built. That line became the inner edge of the north wall of the church. The
next challenge was to get the south wall exactly parallel to it, and the walls and divisions running
across the nave at perfect right angles to it. Brother Hugh did that with Pythagorean triangles.
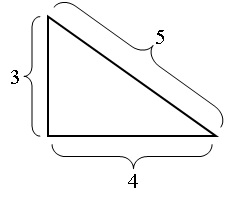
The secret is that some Pythagorean triangles have sides that work out to whole number lengths, and all
Pythagorean triangles include one perfect right angle. The simplest one has a short base of 3, a long
base of 4, and a hypotenuse of 5. Set out a triangle with
these exact proportions ‐ whether the
3, 4, and 5 are inches,
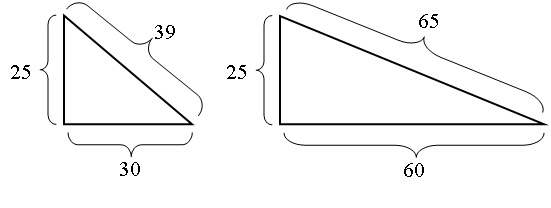
yards, or miles and the angle between the 3 and the 4 will be a perfect right angle. The ones Brother
Hugh used had short bases of 25 medieval English feet. One had a long base of 60 feet and a hypotenuse of
65 feet, and the other one had a long base of 30 feet and a hypotenuse of 39 feet.
So Brother Hugh made the nave 25 feet wide, the western end of the nave 60 feet long, and the eastern end
30 feet long. Make sure all your lengths are correct and you've got perfect right angles, and you
can lay out the south wall to within a couple of inches even if all you’ve got are ropes and wooden
stakes. That's all Hugh had to work with, and he did in fact get it to within a couple of inches.
Once you've got the basic outlines using Pythagorean triangles, the rest can be sketched in using
ropes and stakes; you can do the whole thing within a couple of hours, and get your workmen started
leveling the site and digging the foundation trenches the same day.
Now of course the operative meaning of the 47th proposition of Euclid is far from the only meaning it
has; we are also taught to use the old operative methods for "the more noble and glorious purpose"
of personal and moral improvement. One of the things about Masonic symbolism that makes it so valuable is
that none of the symbols of the Craft just means one thing and one thing only, so there's always
something more to learn. But if we follow our symbols and traditions back to their origins, most of them
relate in one way or another to the operative methods of the builders who built Freemasonry, and that's
a heritage worth remembering.
This article was printed in The Rhode Island Freemason Magazine, March 2019
